A colleague of mine one day went to my office to ask me if I knew about the language Julia. I said I knew the name, but I had never used it till now. He told me something like

You should give it a go, it has all the feature you dream about a language.

HA. What a weird claim to make. You are willing to tell me Julia supports infinite type families???

No but seriously. Julia is a modern language with modern features. And since it is very well possible him and me will work on it at some point, why not give it a go!


[Smooth narrator voice] Krab was not ready for what was to come. Will they survive Julia and its whims? Find out in this SPOOKY TALE OF HALLOW’S EVE!!!

The thing introduces

“Okay Julia”, I told myself. “Let us see what you have got.”

So I went to julialang.org and looked around. On the pain page, you can see the feature of the language that the developers deem the most prominent:

So anyway, a lot of promises, but I am not quite convinced yet. I guess the devs did not think it was relevant to put forward other specificities of Julia, and in particular, Just-in-time compilation, despite it being quite a thing, in my humble opinion.

At this point, I am not too thrilled, let us be honest. But let us see some code alright.


[Smooth narrator voice] And with that, Krab clicked on the manual, as a bolt of lightning cracked the sky in a loud clack.

The interpreter

First things first, Julia comes with its own installation tool, juliaup, that seems to be the go-to platform to install Julia versions and packages.

I am not entirely convinced about specific package managers like that, but why not. It is decently made and seems to work like a charm; good.

The julia command is both the compiler/runner and the interpreter. If you type julia in the command line without any argument, it will fire the REPL.

What a nice REPL!

What a nice REPL!

The REPL is very inviting. I like terminals with colors. It is also modern and ergonomic, especially because you can edit multi-line blocks, go up in the history, and so on. A very nice piece of work!

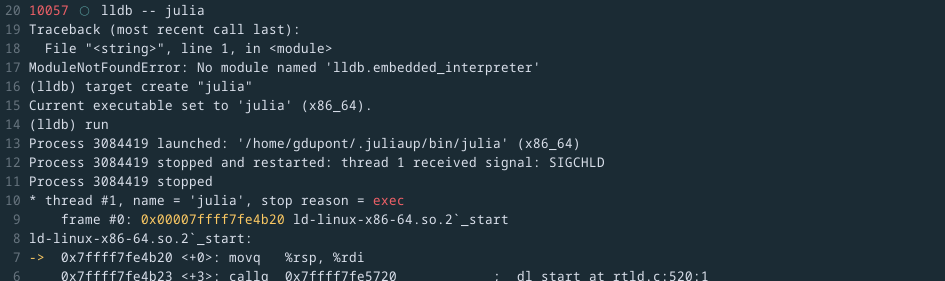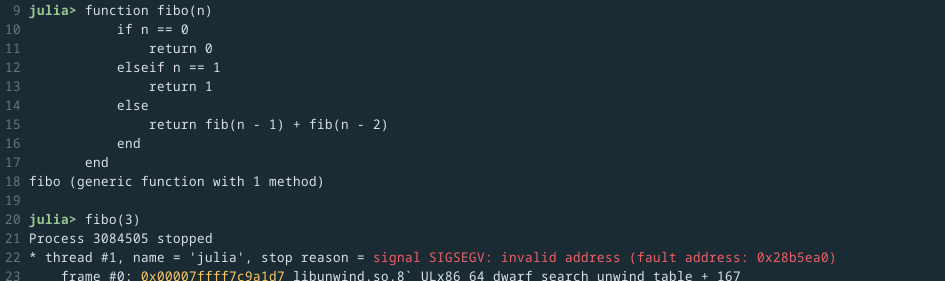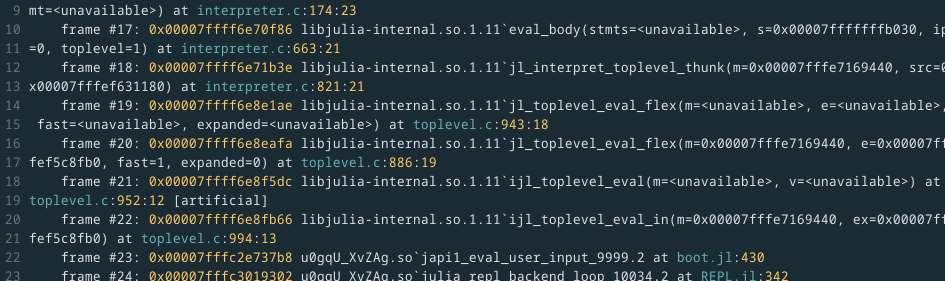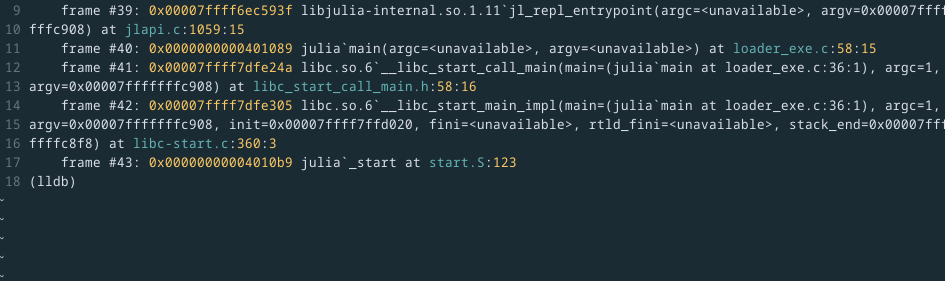
Okay let us write a simple function.

A desperate attempt at Fibonacci

A desperate attempt at Fibonacci


[Smooth narrator voice] Something wrong was afoot. Krab’s little heart was pounding as they observed the result the REPL gave back. Were they a joke to Julia?


Now of course this piece of code cannot work. Look closely, my recursive call is to the function fib instead of fibo. I cannot be mad at Julia that it did not understand what I was saying because what I was saying was dumb!

Well, in fact, yes, I was mad, a little bit. Because. Usually…

…compilers do not crash when the code is wrong.


Seriously. Do I need to fire up the debugger to see why my code is wrong?

What a f\*cking stupid idea

What a f\*cking stupid idea


Okay. Breathe. It is alright. Every compiler/interpreter/whatever this is has its own personality, I find. Haskell’s GHC is a bit of a “HMM, ACTUALLY” kind of person, GCC’s C compiler is a bit of an uncaring parent and its C++ compiler is utterly mad.

So I guess Julia is… Uh… Struggling. Or very mean, I am not sure right now.


Anyway, if you want to now: yes, I noticed the mistake, yes, I fixed it, yes, it worked.

But what a first contact this is.

Julia’s type system

One good thing about Julia is its type system. Yes, the language is dynamically typed, which to me is not always good news, but in the case of Julia (as in the case of Java and for similar reason), this is an important feature of the language.

One thing that I find exciting is that Julia supports the notion of subtyping.

Indeed, Julia lets you define abstract types, and then subtype these types to create a whole type hierarchy!

1
2
3
4
5
6
7
8
9
10
11
12

abstract type Abs end

struct Conc1 <: Abs
  x :: Int64
  y :: Int64
end

abstract type Abs2 <: Abs end

struct Conc2 <: Abs2
  z :: Int64
end

Neat!

“Wait”, I hear you say. “Can you put stuff in an abstract type?”

Nope.

“And… Can you have a struct subtyping another struct?”

Haha, nope.

And I mean, why would you want that? Oh, yes, because it would make sense, uh. Well, whatever, you cannot, and you will have to live with that.


It is alright though – by that I mean that this is not the worst thing in the world. Subtyping is mostly used in conjunction with multiple dispatch; that is, the ability to define several functions with the same name, and have the right one called based on the dynamic type of the argument(s).

1
2
3
4

function f(x :: Abs) ... end
function f(x :: Conc1) ... end
function f(x :: Abs2) ... end
function f(x :: Conc2) ... end

In the example above, whenever calling f, the compiler will select the correct variant based on the type of the argument. In Julia, we say that f is a function, and the various variants of f are methods. My hunch is also that this is the root of the segfault problem I had earlier: when parsing, Julia is not sure about what function exists of not, and it cannot give a definitive answer. That being said, the runtime (especially the REPL) could do the verification and crash with something more meaningful that just a segfault (tell the user what symbol was not defined, typically).


One “consequence” of the multiple dispatch system is that a function is a singleton object of type Function, with basically several apply “generic” methods defined on it, one for each combination of arguments.

I do kind of understand this standpoint but I find it a problem that you cannot specify the input and output type of a function when you are writing higher order function. For instance:

1
2
3

function mymap(x :: T, f :: Function) where T
    return f(x)
end

In this typical scenario, I cannot define the input and output type of the function, and so I cannot declare the output type of mymap, and when calling mymap I cannot make sure the function I pass as the second parameter takes a T as input…

And of course, what happens when I try to execute mymap("abc", x -> x + 5)?

You got it

You got it

The road to define a fix point in Julia

[Smooth narrator voice] And so Krab decided all of that was kind of alright, and to continue their investigation. Their gentle colleague sworn that never, NEVER had he witnessed such segmentation fault, and that maybe, just maybe… It was all Krab’s fault (sike). So Krab went ahead with a crazy idea…

You know what is missing from Julia? A way to write recursive functions using fix points.


Okay so first, let us circumvent the input/output type problem by defining a wrapper for Function:

1
2
3
4
5

struct TFun{From,To}
    fun :: Function
end

mkFun(:: Type{From}, :: Type{To}, f :: Function) where From where To = TFun{From,To}(f)

TFun is for Typed Function. It is basically a normal function annotated with an input (From) and output (To) types. I also define the mkFun constructor, that takes the input and output type as well as the function itself and builds the TFun.

Of course, no verification is made by Julia to check that f is consistent with From and To but the idea is to say that, if the user is reasonable, the thing will work okay.


One thing I find hilarious in Julia is that you may overload function call:

1
2
3

function (f :: TFun{From,To})(x :: From) :: To where From where To
    f.fun(x)
end

With that piece of code, whenever I have myfun :: TFun{A,B} I can write myfun(x) and will call the wrapped function. That is quite neat, in fact!

Now, let us override function composition:

1
2
3

function ∘(f :: TFun{B,C}, g :: TFun{A,B}) where A where B where C 
    mkFun(A, C, f.fun ∘ g.fun)
end

Yes, ∘ is the operator for function composition in Julia (because it is a language for mathematicians). You will note how beautiful it is that we can force the input and output type of the function to ensure type compatibility when doing composition!


And now, for my next trick, let us write the currying transformer!

1
2
3

function curry(f :: TFun{Tuple{A,B},C}) :: TFun{A,TFun{B,C}} where A where B where C
    mkFun(A, TFun{B,C}, a -> mkFun(B, C, b -> f.fun(a,b)))
end

Now, let us do the unthinkable: define a fix point function.

1
2
3

function fix(f :: TFun{TFun{A,B},TFun{A,B}}) :: TFun{A,B} where {A,B}
    mkFun(A,B, x -> f(fix(f))(x))
end

Now a few words on this. 1) It was surprisingly easy to write, 2) It was surprisingly hard to write. In fact, initially, I wanted to write the real fix, with type A → A → A, but I could not :(

I had to resort to write the lesser version, ((A → B) → (A → B)) → A → B.

But anyway, it works! We can write a factorial using that:

1
2
3
4
5
6
7
8
9

function fact_rec(rec :: TFun{Int64,Int64}, n :: Int64) :: Int64
    if n <= 0
        1
    else
        n * rec(n - 1)
    end
end

fact = fix(curry(mkFun(Tuple{TFun{Int64,Int64},Int64},Int64,fact_rec)))

And now…

(╯°□°）╯︵ ┻━┻

(╯°□°）╯︵ ┻━┻

Okay. Right. Julia does not give me a clue about what’s wrong with that. And of course the debugger is… Well I do not want to talk about it okay.


After a long moment of trying stuff out, I figured this worked:

1
2
3

fact_recF = mkFun(Tuple{TFun{Int64,Int64},Int64},Int64,fact_rec)
fact_recC = curry(fact_recF)
fact = fix(fact_recC)

And finally, I can write:

1
2

> fact(5)
120

“Yay!”, I said before laying on the ground and stare at my ceiling for a solid hour.

Conclusion

[Smooth narrator voice] And so Krab achieved his descent into madness, writing a stupid operator nobody asked for in a language that clearly does not like them. But needless to say, they could not even begin to fathom what was to come…


So yeah, in fact, Julia is a neat language. I think it suffers from being a bit “young” (although it has been around for more than a decade), and maybe a user base that is mostly concerned by mathematics, and do not really push the language past its limit (maybe?).

Julia wants to be the successor of Python and Matlab, and, quite frankly, I hope it will be. I could ramble hours about how Python and Matlab are terrible, terrible languages, and it is true that, at least on paper, Julia is fixing most of the problems they exhibit.

I can only hope for a wider adoption of this language, which will inevitably lead to more improvements and more features.

In the end, I find it to be quite a reasonable modern language, even though there is no trait or object system in it (sigh).



Wait what is to come and why cannot I fathom it??