As you may have noticed in a previous post, I might be, what you may call, crazy about combinators. This is even more strange since I do not really like language theory as a whole.
But parsers and parser combinators? Ooooooooh boy. Delicious.
So anyway, today we are making a parser combinator library in Java. This is a ridiculous task, especially because there is a little thing called ANTLR that generate parsers from a grammar with no issue.
But you know what, I think a good language is a language where I can do parser combinators, and I think Java is a good language, so here we go.
Parser combinators: a short summary
In the aforementioned previous post, we delved into what where parser combinators, or what I like to call a parser combinator system, which to me is an algebra of parsers together with atomic or elementary parsers.
A parser is a box that takes a stream as input and outputs the remainder of the stream minus what it has parsed and a result it has calculated from the stream, if successful.
Elementary parsers are usually able to fulfil a simple task, typically telling if a character is right or not (i.e., satisfying a predicate), telling if the stream has reached its end, and so on. When a parser finds that the condition it revolves around is satisfied, then it yields a success result; otherwise, it yields a failure result.
From there, we can combine parsers to obtain more complex parsers, with this failure-success semantics, in three main ways:
- Sequencing P . Q, which succeeds if and only if P and then Q succeed
- Alternative P + Q, which succeeds if either P or Q succeeds
- Repetition P*, which always succeeds and “runs” as many time as possible
To that we add the parser that always fails 0 and the parser that always succeeds with a value 1(…), a few interesting properties, and that is it! We got ourselves a Kleene Algebra. Yay!
Cruxes of the implementation
Believe it or not the final parser combinator system I ended up with in Java is not that complicated; but a lot – and I mean, a lot – of time went in designing it, so that is has a nice “codefeel” to it.
The first driving force behind the design choices for this simple lib is that I do not want the user to create a parser by calling a bunch of constructors.
Do not get me wrong, constructors are nice and stuff but I want to keep a functional-like quality to the parsers, in something that is more akin to Java streams. Typically, I want to be able to do stuff such as this:
The other thing we need to watch out is that Java does not support recursive
values, and is not lazy by default. This means that p = x.then(p) or even
p() { return x.then(p()); } is out of the question.
We will have to do “lazy by hand”. In our case, we want to avoid parsers being “evaluated” (that is, functions returning a parser being called) when it is not necessary.
This is something that can be achieved without getting our hands into some
complex laziness implementation stuff, simply by having parsers be given as
Suppliers.
That way, stuff like p1.then(p2) becomes p1.then(() -> p2), effectively
“freezing” p2 until and if needed.
The streams
As with Haskell, the first thing we are going to look into is the notion of
stream. The easiest way of handling a generic stream of character is with an
interface. In this interface, we want a next operation that yields the next
symbol, and an eos getter to determine if we are done with the stream.
Unlike in Haskell, our streams will be very much stateful, closer to iterators than to functional lists. This is because it is easier to handle, and much more efficient in term of memory (having purely functional streams would duplicate a lot of memory all around the place).
This also means that we can do “efficient branching” using a type that holds the state of a stream, that can be resumed afterwards. This is especially useful for alternative parser combinators.
Let us see what it looks like:
1 2 3 4 5 6 7 8 9 |
public interface Stream<Symbol> { public interface StreamSnapshot<Symbol> {} Optional<Symbol> next(); boolean eos(); StreamSnapshot<Symbol> snap(); void conflate(StreamSnapshot<Symbol> snap); } |
The “snapshot” part is to do the branching: snap creates a record point (a
checkpoint in a way) and conflate put the stream back in the state represented
by the snapshot.
Now there are a number of possible implementations for streams; I will not discuss it here. As always, all my code is made available on my GitHub.
The main Parser type
This takes care of most of the technical issues we are going to stumble across, but an important thing remains: how do we efficiently model a parser in Java.
Like for the parsers in Haskell, we will have a Stream object that represent
the flux of characters we want to parse. Obviously, a parser needs to access
said stream. Considering we want to chain parsers in a stream kind of way, we
will be creating parsers “on-the-fly”, and so streams cannot be attributes of
parsers; it has to be passed as argument.
Since we want to chain parsers, the stream should be provided to the next parsers by the previous ones, and combinators should take care of “branching” and managing the streams wherever it must go.
In addition to the stream being passed on, we will also pass a state, to allow for stateful parsers. We did not have to do that in Haskell because the state was already a polymorphic type, but here it will not be. This is a good opportunity to talk a bit about stateful parsers, which allow more complex grammars to be built, but we will see that later.
So, putting everything together, a parser takes as input a state and a stream, and outputs a result, the update state and the updated stream, if successful.
This means what we will first need a ParserResult type, that may be either a
success or a failure, or an error if we want to notify the user something went
wrong (just a reminder that failure is a state of the parser that can happen
organically, while error is a crash that is not supposed to happen).
If we want to be as generic as possible, we will abstract the symbols, the state
and the result by generic types (Sym, St and R, respectively).
In Haskell, we had sum-types, in Java we do not; but we have the union type design pattern:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
public class ParserResult<Sym,St,R> { public static final class Success<Sym,St,R> extends ParserResult<Sym,St,R> { public final Stream<Sym> stream; public final St state; public final R result; Success(Stream<Sym> str, St st, R res) { this.stream = str; this.state = st; this.result = res; } @Override public boolean isSuccess() { return true; } @Override public boolean isFailure() { return false; } @Override public boolean isError() { return false; } } public static final class Failure<Sym,St,R> extends ParserResult<Sym,St,R> { Failure() {} @Override public boolean isSuccess() { return false; } @Override public boolean isFailure() { return true; } @Override public boolean isError() { return false; } } public static final class Error<Sym,St,R> extends ParserResult<Sym,St,R> { public final ParserError<Sym> error; Error(ParserError<Sym> err) { this.error = err; } @Override public boolean isSuccess() { return false; } @Override public boolean isFailure() { return false; } @Override public boolean isError() { return true; } } public abstract boolean isSuccess(); public abstract boolean isFailure(); public abstract boolean isError(); ... } |
You may have noticed that the constructors of the subclass have a package reach. This is because the user should not call the constructor themselves; instead, they should use one of the static maker method:
1 2 3 4 |
public static <Sym,St,R> ParserResult<Sym,St,R> success(Stream<Sym> stream, St state, R value) { return new Success<Sym,St,R>(stream, state, value); } ... // And so on |
Just like in Haskell, this ParserResult type is monadic in nature. To make it
easier on ourselves later, it is a good idea to define a transformer akin to the
monadic bind:
1 2 3 4 5 6 7 8 9 10 |
public final <R2> ParserResult<Sym,St,? extends R2> chain(StateStreamFunction<Sym,St,? super R,? extends ParserResult<Sym,St,R2>> then) { if (this.isSuccess()) { Success<Sym,St,R> succ = (Success<Sym,St,R>) this; return then.apply(succ.stream, succ.state, succ.result); } else if (this.isFailure()) { return failure(); } else { return error(((Error<Sym,St,R>) this).error); } } |
Where StateStreamFunction is a functional interface representing a function of
stream, state and result (i.e., exactly what is inside a ParserResult:
1 2 3 4 |
@FunctionalInterface public interface StateStreamFunction<Sym,St,RIn,ROut> { ROut apply(Stream<Sym> stream, St state, RIn result); } |
You will notice that we use bounded type parameters in the signature. This is mostly to allow covariance and contravariance, i.e. a little bit of flexibility on what types are allowed as input and output of the function.
With all that, we can finally define our parser type:
1 2 3 |
public interface Parser<Sym,St,R> { ParserResult<Sym,St,? extends R> parse(Stream<Sym> stream, St state); } |
Easy, right?
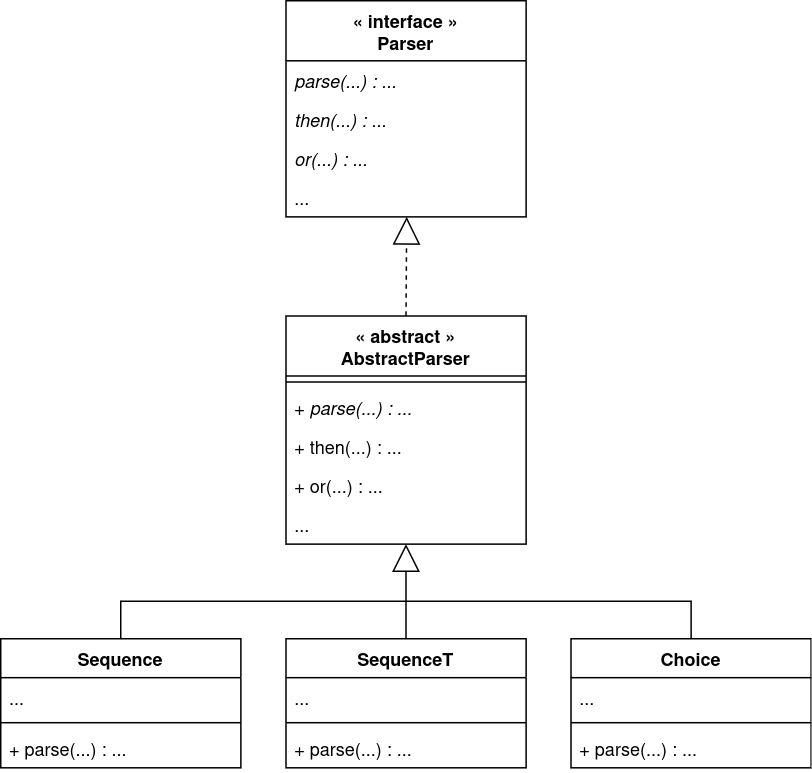
The combinators
Now that we have a type for parsers, we may introduce combinators. The
combination of two parsers is a parser, so a combinator is a class that holds
two parsers and is itself an implementation of Parser.
As hinted before, we need to make sure the parsers in the combinator are “lazy”, in the sense that we may delay (possibly indefinitely) their evaluation to the last moment.
Let us see how this plays out for the sequence combinator:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
public class Sequence<Sym,St,R1,R2> extends AbstractParser<Sym,St,R2> { public final Parser<Sym,St,? extends R1> left; public final Supplier<Parser<Sym,St,? extends R2>> right; public Sequence(Parser<Sym,St,? extends R1> left, Supplier<Parser<Sym,St,? extends R2>> right) { this.left = left; this.right = right; } @Override public ParserResult<Sym,St,? extends R2> parse(Stream<Sym> stream, St state) { return this.left.parse(stream, state).chain( (str,st,res) -> this.right.get().parse(stream, state) ); } } |
We see here the use of Supplier for “laziness”, and also the use of various
bounds on the type parameters, again to allow leeway when combining parsers.
The main parse method is straightforward: run left then right, exploiting
the chain method of the ParserResult class.
Note that the result of the first parser is discarded. Ideally, we would want to
create a variant of Sequence where the second parser is “calculated” from the
result of the previous (basically modelling the monadic bind of parsers).
This is what I came up with, very simply:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
public class SequenceT<Sym,St,R1,R2> extends AbstractParser<Sym,St,R2> { private Parser<Sym,St,R1> left; private StateStreamFunction<Sym,St,R1,Parser<Sym,St,? extends R2>> right; public SequenceT(Parser<Sym,St,R1> left, StateStreamFunction<Sym,St,R1,Parser<Sym,St,? extends R2>> right) { this.left = left; this.right = right; } @Override public ParserResult<Sym, St, ? extends R2> parse(Stream<Sym> stream, St state) { return this.left.parse(stream, state).chain( (str,st,res) -> this.right.apply(str,st,res).parse(stream, state) ); } } |
I find this version of the monadic bind to be more powerful than the one proposed in Haskell, the reason being that the parser may be calculated based on the state and on the stream in addition to on the result. This is of course a double-edge blade, as we may write very incomprehensible parsers with that…
The alternative combinator is not very complicated once you recall the feature of streams of having checkpoints or snapshots:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
public class Choice<Sym,St,R> extends AbstractParser<Sym,St,R> { public final Parser<Sym,St,? extends R> left; public final Supplier<Parser<Sym,St,? extends R>> right; public Choice(Parser<Sym,St,? extends R> left, Supplier<Parser<Sym,St,? extends R>> right) { this.left = left; this.right = right; } @Override public ParserResult<Sym,St,? extends R> parse(Stream<Sym> stream, St state) { // Create a check point in the stream to go back to if left fails StreamSnapshot<Sym> current = stream.snap(); ParserResult<Sym,St,? extends R> lr = this.left.parse(stream, state); if (lr.isFailure()) { stream.conflate(current); // Restore the save return this.right.get().parse(stream, state); } else { return lr; } } } |
Once again, we use Suppliers to allow laziness for such parser as P = x | P
(careful, laziness on the RHS only, since
the LHS is always evaluated first anyway).
You will note that if the result of the LHS is an error then the error is propagated (an error is not a failure).
I will just note that there is a fourth combinator I will not delve into that
takes a parser and a StateStreamFunction and maps that function to the result
of the parser (essentially realizing the functorial map for parsers), called
ParserT.
Stream-ification
As mentioned earlier, I do not want the user to write stuff like
1 |
new Sequence(new Sequence(new Alternative(...), ...), ...) |
I want a stream-like notation, in the Java sense:
1 |
p0.or(p1.then(() -> p2), () -> p3.then(() -> p4)) |
How do we do that? Not very difficult: we add methods such as or and then to
the Parser interface. The problem then is that they must be implemented for
every parser, and it is a bit tedious; but we can factor a lot of code by using
an adapter, that is an abstract
class that is a “partial implementation” of Parser and that other parsers may
subclass.
The use of an adapter is really a good idea. I do not mean only here where it enables adding features to parsers while having to maintain only one class and one interface, but also in general; this is truly one of my favourite design patterns.
In term of code, nothing particularly new, in fact:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
public abstract class AbstractParser<Sym,St,R> implements Parser<Sym,St,R> { @Override public Parser<Sym,St,R> or(Supplier<Parser<Sym,St,? extends R>> right) { return new Choice<Sym,St,R>(this, right); } @Override public <R2> Parser<Sym,St,? extends R2> then(Supplier<Parser<Sym,St,? extends R2>> right) { return new Sequence<Sym,St,R,R2>(this, right); } @Override public <R2> Parser<Sym,St,? extends R2> then(StateStreamFunction<Sym,St,R,Parser<Sym,St,? extends R2>> right) { return new SequenceT<Sym,St,R,R2>(this, right); } ... } |
Of course, one may notice that, although the stream notation is very good for
thens, it is not as good for or (although this is a matter of taste). You
may also have noticed that we have not defined any elementary parser too…
What we need right now is a “complementary” utility class that gather all the
features we need – typically, a Parsers class (Java convention):
1 2 3 4 5 6 7 |
abstract public class Parsers { private Parsers() {} // The class is not intended to be instanciated public static <Sym,St,R> Parser<Sym,St,R> or(Parser<Sym,St,? extends R> left, Parser<Sym,St,? extends R> right) { return new Choice<Sym,St,R>(left, () -> right); } } |
Let us define the end of stream parser, quite simply:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
public static class EOS<Sym,St> extends AbstractParser<Sym,St,Void> { @Override public ParserResult<Sym, St, Void> parse(Stream<Sym> stream, St state) { if (stream.eos()) return ParserResult.success(stream, state, null); else return ParserResult.failure(); } } public static <Sym,St> Parser<Sym,St,Void> eos() { return new EOS<Sym,St>(); } |
Notice that, thanks to our adapter, we can even write parsers as anonymous
subclasses. For instance, let us write ret (1(…)) and fail (0):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
public static <Sym,St,R> Parser<Sym,St,R> ret(R value) { return new AbstractParser<Sym,St,R>() { @Override public ParserResult<Sym,St,? extends R> parse(Stream<Sym> stream, St state) { return ParserResult.success(stream, state, value); } }; } public static <Sym,St,R> Parser<Sym,St,? extends R> fail() { return new AbstractParser<Sym,St,R>() { @Override public ParserResult<Sym, St, ? extends R> parse(Stream<Sym> stream, St state) { return ParserResult.failure(); } }; } |
The next logical step is to define the predicate parser and its equality
specialization, called is(Predicate<Sym>) and is(Sym), as well as other
elementary parser for matching a sequence for example, and so on and so on.
Just because I can and because I find it fun, let us define a variadic version
of or:
1 2 3 4 5 6 7 8 9 10 11 12 |
@SafeVarargs public static <Sym,St,R> Parser<Sym,St,? extends R> or(Parser<Sym,St,? extends R>... parsers) { if (parsers.length == 0) { return Parsers.fail(); } else { Parser<Sym,St,? extends R> current = parsers[0]; for (int i = 1; i < parsers.length; i++) { current = or(current, parsers[i]); } return current; } } |
That way we can write such things as or(p1, p2, p3, p4, p5) (and it wraps the
parsers in Suppliers as well!).
Examples
I will be honest, I was not convince my lib would work. In fact, it all may seem quite easy when you look at it, but there was a lot of tweaking involved (especially with type bounds and “laziness”). But in the end, it works! It even works quite well, in fact!
The first basic test: basic number parsing
Parsing a number is easy: a number is a stream of digits, a digit is any
character between '0' and '9' (or any character that satisfies
Character.isDigit, more simply). If I had to give a formal grammar, this would
be it:
The main issue is to capture the digits and reconstitute the number, which can be done with a bunch of monadic chaining, using the result as a sort of accumulator.
Here is what it looks like:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
// Parse one digit (not recursive, so can be a value) private static Parser<Character,Void,? extends Integer> parseDigit = Parsers.<Character,Void>is(c -> Character.isDigit(c)).map((stream, state, c) -> Character.digit(c, 10)); // Parse a number (recursive, so must be a function) private static Parser<Character,Void,? extends Integer> parseNumber(int acc) { return parseDigit.then((str,st,d) -> Parsers.or( parseNumber(acc * 10 + d), // Still have more to parse (NS → digit NS) Parsers.ret(acc * 10 + d) // Nothing else to parse (NS → Λ) )); } // The "root" parser, starting with the accumulator at 0 private static Parser<Character,Void,? extends Integer> parseNumber = parseNumber(0); |
A bit of parsing boilerplate to execute the parser:
1 2 3 4 5 6 7 8 9 10 11 12 |
private static <E> ParserResult<Character,Void,? extends E> doParse(Parser<Character,Void,E> parser, String input) { RandomAccessList<Character> tokens = new RandomAccessList<>(); tokens.addAll(input.chars().mapToObj(c -> (char) c).collect(Collectors.toList())); // Turn the input into a Stream return parser.parse(new SharedStream<Character>(tokens), null); } public static void main(String[] args) { System.out.println("120 => " + doParse(parseNumber, "120")); System.out.println("7 => " + doParse(parseNumber, "7")); System.out.println("87981a => " + doParse(parseNumber, "87981a")); System.out.println("a => " + doParse(parseNumber, "a")); } |
And… Victory!!
Real-world parsing: expressions to AST
Of course parsing numbers is fun and all; but this is Java, a serious language for serious people, right? So if my library is serious it should be able to do serious things, such as parsing a stream of token and outputting an abstract syntax tree (AST).
Let us consider the language of propositional logic. What we want is something that transforms a stream of tokens (variables, conjunction, disjunction, implication, equivalence) into a syntax tree:
This is really typical of what grammars are for. If we can manage this, we can parse anything (or almost anything). The formal grammar we want to implement is the following:
1 2 3 4 5 6 7 8 9 10 |
Expr → Impl => Expr Expr → Impl <=> Expr Expr → Impl Impl → Term \/ Impl Impl → Term Term → Factor /\ Term Term → Factor Factor → ( Expr ) Factor → ~ Factor Factor → variable |
We thus have the tokens =>, <=>, \/, /\, (, ) and variable, and
four functions (the grammar is recursive) to write, plus one to parse variables,
just for convenience.
Here is what I came up with:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
public static Parser<Token,Void,? extends Expr> parseVariable() { return Parsers.<Token,Void>is(t -> t instanceof VarToken).then((stream,state,r) -> Parsers.ret(new Var(r.getContent()))); } public static Parser<Token,Void,? extends Expr> parseFactor() { return Parsers.<Token,Void,Expr>or( Parsers.<Token,Void>is(OPAREN) .then(() -> parseExpr() .<Expr>then((stream,state,val) -> Parsers.<Token,Void>is(CPAREN).<Expr>ret(val))), Parsers.<Token,Void>is(NOT) .then(() -> parseFactor() .then((stream,state,val) -> Parsers.ret(new UnOp(UnOp.Op.NOT, val)))), parseVariable() ); } public static Parser<Token,Void,? extends Expr> parseTerm() { return Parsers.<Token,Void,Expr>or( parseFactor().then((stream,state,val) -> Parsers.<Token,Void>is(AND) .then(() -> parseTerm() .then((stream2,state2,val2) -> Parsers.ret(new BinOp(BinOp.Op.AND, val, val2))))), parseFactor() ); } public static Parser<Token,Void,? extends Expr> parseImpl() { return Parsers.<Token,Void,Expr>or( parseTerm().then((stream,state,val) -> Parsers.<Token,Void>is(OR).then(() -> parseImpl() .then((stream2,state2,val2) -> Parsers.ret(new BinOp(BinOp.Op.OR, val, val2))))), parseTerm() ); } public static Parser<Token,Void,? extends Expr> parseExpr() { return Parsers.<Token,Void,Expr>or( parseImpl().then((stream,state,val) -> Parsers.<Token,Void>is(IMP) .then(() -> parseExpr().then((stream2,state2,val2) -> Parsers.ret(new BinOp(BinOp.Op.IMP, val, val2))))), parseImpl().then((stream,state,val) -> Parsers.<Token,Void>is(EQV) .then(() -> parseExpr().then((stream2,state2,val2) -> Parsers.ret(new BinOp(BinOp.Op.EQV, val, val2))))), parseImpl() ); } |
And here we go! It parses! It is alive, ALIVE!
I would be lying if I told you this was easy to write. In fact, the main
skeleton of the parser is relatively easy to come up with, as it follows the
grammar pretty well. The main issue is typing. Because we have a lot of type
parameters and Java’s type inference is weak, we sometimes have to add type
annotations, especially for static functions (e.g., is).
But once you are used to it, writing parsers is as hard as writing Java could be, so neither too hard nor too easy, somewhere in the middle…
Stateful parsing
In the two previous examples, we had parsers that did not use the state
argument. Let us see how it can be used for the benefit of mankind.
Before we can do that, we must add two new combinators for handling the state in
parsers. The first is called commit, it alters the state in the parser chain
using a function of the former state and of the result:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
public Parser<Sym,St,? extends R> commit(BiFunction<R,St,St> fun) { return new AbstractParser<Sym,St,R>() { @Override public ParserResult<Sym, St, ? extends R> parse(Stream<Sym> stream, St state) { ParserResult<Sym,St,? extends R> r = AbstractParser.this.parse(stream, state); if (r.isSuccess()) { St st = fun.apply(r.getResult().get(), state); return ParserResult.success(stream, st, r.getResult().get()); } else { return r; } } }; } |
Then, extract retrieve something from the state and the result and put it in
the result of the parser:
1 2 3 4 5 6 7 8 9 |
public <R2> Parser<Sym,St,? extends R2> extract(BiFunction<R,St,R2> fun) { return new AbstractParser<Sym,St,R2>() { @Override public ParserResult<Sym, St, ? extends R2> parse(Stream<Sym> stream, St state) { ParserResult<Sym,St,? extends R> r = AbstractParser.this.parse(stream, state); return r.map(res -> fun.apply(res, state)); } }; } |
This could have been proper classes, but I found it far too specific for that (but maybe it should).
Basically, commit is what allows us to write in the state, while extract is
what allows us to output parts of the state in the result of the parser.
As an example, imagine writing a parser for lexing
a stream of characters (for instance, a stream of +, * and numbers).
One could use the result of the parsers to build a list of tokens from the input; but in Java, lists are inherently mutable and with side effects. Thus, this is better handled using a state: the state is the list of tokens thus parsed, upon successfully parsing a token, we commit to the state by adding the new token to the list. When we reach the end of the stream, we extract the state and return it as the result of the parser, and that is it!
Let us see how it goes:
1 2 3 4 5 6 7 8 9 |
public static Parser<Character,List<Token>,? extends List<Token>> parseString() { return Parsers.<Character,List<Token>,List<Token>>or( parseNumber(0).commit((i, l) -> { l.add(new NumberToken(i)); return l; }).then(() -> parseString()), Parsers.<Character,List<Token>>is('+').commit((x, l) -> { l.add(new PlusOp()); return l; }).then(() -> parseString()), Parsers.<Character,List<Token>>is('*').commit((x, l) -> { l.add(new TimesOp()); return l; }).then(() -> parseString()), Parsers.<Character,List<Token>>is(c -> Character.isSpaceChar(c)).then(() -> parseString()), Parsers.<Character,List<Token>>eos().extract((x, st) -> st) ); } |
Believe it or not, this is far, far less messy than combining lists in monadic binds! And it works like a charm too :3
1 2 3 4 |
Parsing input: 123+451 Success: [<123>, <+>, <451>] Parsing input: 12 + 5 * 3 Success: [<12>, <+>, <5>, <*>, <3>] |
Conclusion
And voilà! We made a parser combinators library in Java, exploiting the power of object-oriented programming and of “lambda expressions” to build up a library that is simple, relatively ergonomic and quite powerful!
I did not touch on the performances of this library, because I did not really benchmark it. I suspect that is might be catastrophic memory-wise, because we create a lot of layers of parsers. Time-wise, it should be relatively okay, especially with function inlining and stuff like that.
Of course, it would be better if Java had real lambda expressions where side effects were forbidden, but oh well, we cannot have everything.
As always my code is available on GitHub if you want to take a look and delve in the untold specifics of this little project.
I hope you had fun! :3